SVMs are useless?

What are SVMs?

How do we separate negatives examples from positive examples? Widest Street Approach to separate between negatives and positives

How do you make decision rule to make a decision boundary?

Let’s make a vector parpendicular to the median & say we have another unknown

If the projection of that random vector is too big and if it’s too big than it must be in positive side

w(vec) . u(vec) + b >= 0  then it's a positive sample --> Decision Rule

where,

w(vec) = parpendicular
u(vec) = random point and vector from median

If we take,

w(vec) . x(some positive sample) + b >= 1

likewise

w(vec) . x(some negative sample) + b <= -1

so, lets introduce a variable y

yi such that yi = +1 for + samples -1 for - samples

y_i (x_i . w + b) >= 1
y_i (x_i . w + b) >= 1 (why is it positive?)

y_i (x_i . w + b) -1 >= 0

For x_i in gutter(it’s the middle road. Any sample lying in road should be zero)

y_i (x_i . w + b) -1 = 0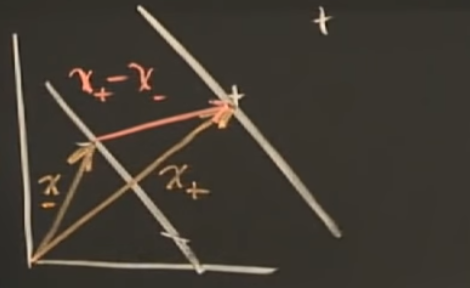

so what’s the width of street?

WIDTH = (x+ - x-) . w(vec)/ w(magnitude)